Difference Between Fuzzy Set and Crisp Set

Fuzzy set and crisp set are the part of the distinct set theories, where the fuzzy set implements infinite-valued logic while crisp set employs bi-valued logic. Previously, expert system principles were formulated premised on Boolean logic where crisp sets are used. But then scientists argued that human thinking does not always follow crisp “yes”/”no” logic, and it could be vague, qualitative, uncertain, imprecise or fuzzy in nature. This gave commencement to the development of the fuzzy set theory to imitate human thinking.

For an element in a universe, that comprise fuzzy sets can have a progressive transition among several degrees of membership. While in crisp sets the transition for an element in the universe between membership and non-membership in a given set is sudden and well defined.

Content: Fuzzy Set Vs Crisp Set

1. 1. Comparison Chart
   2. Definition
   3. Key Differences
   4. Conclusion

Comparison Chart

Basis for comparison	Fuzzy Set	Crisp Set
Basic	Prescribed by vague or ambiguous properties.	Defined by precise and certain characteristics.
Property	Elements are allowed to be partially included in the set.	Element is either the member of a set or not.
Applications	Used in fuzzy controllers	Digital design
Logic	Infinite-valued	bi-valued

Definition of Fuzzy Set

A fuzzy set is a combination of the elements having a changing degree of membership in the set. Here “fuzzy” means vagueness, in other words, the transition among various degrees of the membership complies that the limits of the fuzzy sets are vague and ambiguous. Therefore, the membership of the elements from the universe in the set is measured against a function to identify the uncertainty and ambiguity.

A fuzzy set is denoted by a text having tilde under strike. Now, a fuzzy set X would contain all the possible outcome from interval 0 to 1. Suppose a is an element in the universe is a member of fuzzy set X, the function gives the mapping by X(a) = [0,1]. The notion convention used for fuzzy sets when the universe of discourse U (set of input values for the fuzzy set X) is discrete and finite, for fuzzy set X is given by: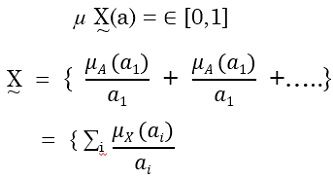The fuzzy set theory was initially proposed by a computer scientist Lotfi A. Zadeh in the year of 1965. After that lot of theoretical development has been done in a similar field. Previously the theory of crisp sets based in dual logic is used in the computing and formal reasoning which involves the solutions in either of two form such as “yes or no” and “true or false”.

Fuzzy logic

Unlike crisp logic, in fuzzy logic, approximate human reasoning capabilities are added in order to apply it to the knowledge-based systems. But, what was the need to develop such a theory? The fuzzy logic theory provides a mathematical method to apprehend the uncertainties related to the human cognitive process, for example, thinking and reasoning and it can also handle the issue of uncertainty and lexical imprecision.

Example

Let’s take an example to understand fuzzy logic. Suppose we need to find whether the colour of the object is blue or not. But the object can have any of the shade of blue depending on the intensity of the primary colour. So, the answer would vary accordingly, such as royal blue, navy blue, sky blue, turquoise blue, azure blue, and so on. We are assigning the darkest shade of blue a value 1 and 0 to the white colour at the lowest end of the spectrum of values. Then the other shades will range in 0 to 1 according to intensities. Therefore, this kind of situation where any of the values can be accepted in a range of 0 to 1 is termed as fuzzy.

Definition of Crisp Set

The crisp set is a collection of objects (say U) having identical properties such as countability and finiteness. A crisp set ‘B’ can be defined as a group of elements over the universal set U, where a random element can be a part of B or not. Which means there are only two possible ways, first is the element could belong to set B or it does not belong to set B. The notation to define the crisp set B containing a group of some elements in U having the same property P, is given below. It can perform operations like union, intersection, compliment and difference. The properties exhibited in the crisp set includes commutativity, distributivity, idempotency, associativity, identity, transitivity and involution. Though, fuzzy sets also have the same above given properties.

Crisp Logic

The traditional approach (crisp logic) of knowledge representation does not provide an appropriate way to interpret the imprecise and non-categorical data. As its functions are based on the first order logic and classical probability theory. In another way, it can not deal with the representation of human intelligence.

Example

Now, let’s understand the crisp logic by an example. We are supposed to find the answer to the question, Does she have a pen? The answer of the above-given question is definite Yes or No, depending on the situation. If yes is assigned a value 1 and No is assigned a 0, the outcome of the statement could have a 0 or 1. So, a logic which demands a binary (0/1) type of handling is known as Crisp logic in the field of fuzzy set theory.

Conclusion

The fuzzy set theory is intended to introduce the imprecision and vagueness in order to attempt to model the human brain in artificial intelligence and significance of such theory is increasing day by day in the field of expert systems. However, the crisp set theory was very effective as the initial concept to model the digital and expert systems working on binary logic.