Difference Between DTE and DCE

DTE (Data terminating equipment) and DCE (Data circuit terminating equipment) both terms are frequently used in Data communication and networking; these terms can be considered as the type of serial communication devices where basic WAN connectivity between subscriber and provider relies on.

The basic difference between DTE and DCE is that DCE is usually located at the service provider whereas DTE is the attached device.

Content: DTE Vs DCE

1. Comparison Chart
2. Definition
3. Key Differences
4. Conclusion

Comparison Chart

Basis for comparison	DTE	DCE
Basic	A device that is an information source or an information sink.	A device used as an interface between a DTE.
Primary functions	Produces the data and transfers them to a DCE, with essential control characters.	Converts the signals to a format appropriate to the transmission medium and introduces it onto the network line.
Coordination	No coordination is required between DTE devices.	DCE devices must be coordinated in order to communicate.
Included devices	Routers and computers	Modem
Relation	Connected through the help of a DCE network.	DCE network acts as a medium for two DTE networks.

Definition of DTE

DTE (Data terminating equipment) is a terminal residing at physical layer or can be anything that could be able to generate to consume digital data like computers. In other words, it is an assembly that operates either as a source of or as a destination for binary digital data. There is no direct mechanism for DTE to communicate, so communication occurs place through some intermediary devices.

Example

Let’s take a real life example which will illustrate the working of DTE. Suppose your brain is a DTE device which can generate and consume ideas. If your brain wants to communicate with your friend’s brain to interpret the idea generated by your brain, It would not be practically possible. Consequently, your brain will take help of your vocal chords for the interpretation of the idea. That’s how a DTE works.

Customer devices that connect to the telephone company’s (telco’s) equipment are known as CTE(Customer telephony Equipment). Demarcation point (demarc) is the meeting spot of customer equipment (DTE) and telephone equipment (DCE).

Definition of DCE

DCE (Data circuit terminating equipment) involves operative units that transfer or receives data in the form of digital or analog signal within a network. In the physical layer, the DCE obtain the data produced by the DTE and convert it to suitable signals. Then it introduce the signal onto the telecommunication link. Generally, the DCE’s we use at this layer involves modems (modulator/demodulator).

In a network, a DTE produces digital data and move them to a DCE. Then DCE translates the data in a specific form that can be accepted by the transmission medium and sends the translated signal to another DCE on the network. The second DCE extracts the signal out of the line, and transforms it into such a form that its DTE can use and deliver.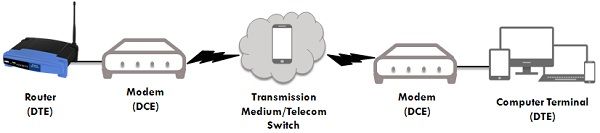 In order to achieve this communication, both the sending and receiving DCEs must use the same modulating method (e.g., FSK), much the way that if you want to communicate to someone who understands one particular language, then you must speak the particular language.

There is no compulsion to synchronize the two DTEs with each other, but each must be coordinated with its own DCE, and the DCEs must be coordinated so that data translation occurs without loss of integrity.

Conclusion

DTE (Data terminating equipment) and DCE (Data circuit terminating equipment) are the types of serial communication devices.

Both DCE and DTE devices are equally important for WAN connectivity. DTE is a device which can perform as a binary digital data source or destination. While DCE includes devices that transmit or receives data in the form of digital or analog signal in a network.