Difference Between One-Dimensional (1D) and Two-Dimensional (2D) Array

An array is a collection of variables that are of similar data types and are alluded by a common name. The main topic of our discussion is the difference between One-dimension and Two-Dimension array. A one-dimensional array is a list of variables with the same data type, whereas the two-Dimensional array is ‘array of arrays’ having similar data types.

A specific element in an array is accessed by a particular index of that array. Arrays in Java work differently as compared to C++. C++ do not have bound checking on arrays whereas, Java have strict bound checking on arrays.

There are several factors according to which the one-dimensional and two-dimensional arrays can be differentiated, such as the way these are initialized, accessed, implemented, inserted, deleted, traversed. So, let’s begin with the differences between One-dimension and Two-Dimension array along with a comparison chart.

Content: One-Dimensional (1d) Vs Two-dimensional (2d) Array

1. Comparison Chart
2. Definition
3. Key Differences
4. Calculation of address
5. Conclusion

Comparison Chart

Basis for Comparison	One-Dimensional	Two-Dimensional
Basic	Store single list of elements of similar data type.	Store 'list of lists' or 'array of arrays' or 'array of one dimensional arrays'.
Declaration	/*declaration in C++ type variable_name[ size ];*/ /*declaration in Java type variable_name [ ]; variable_name = new type[size]; */	/*declaration in C++ type variable_name[size1][size2]; */ /*declaration in Java type variable_name= new int[size1][size2]; */
Alternative Declaration	/* In Java int [ ] a= new int [10]; */	/* In Java int [ ] [ ] a= new int [10][20]; */
Total Size in Bytes	Total Bytes =sizeof(datatype of array variable)* size of array.	Total Bytes= sizeof(datatype of array variable)* size of first index*size of second index.
Receiving parameter	It can be received in a pointer, sized array or an unsized array.	Parameter receiving it should define the rightmost dimension of an array.
Dimensions	One dimensional.	Two dimensional.

Definition of One-Dimensional Array (1-D array)

One-Dimensional or Single-Dimensional array is considered as the ”list of variables of similar data types”, and each variable can be distinctly accessed by specifying its index in square brackets preceded by the name of that array.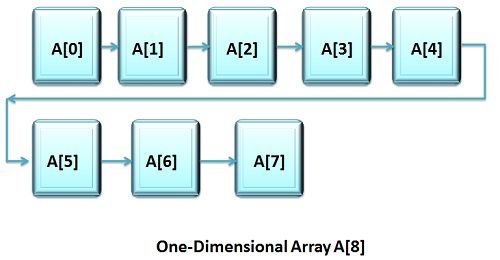 In C++, the declaration of an array variable with the size is enough to allocate space for them in memory. In Java, this is achieved in two steps. First, you must declare a variable of the desired type. Second, you must allocate the memory to hold the array using ‘new’ and assign it to the declared array variable. Hence, arrays are dynamically allocated in Java.

Declaration of 1D Array in C++

Let’s discuss in C++ Context

//declaration in C++
type variable_name[ size ];

Here type declares the data type of array variable, and size defines the number of elements that array will hold. For example, if we want to declare an array which will contain the balance of each month of the year.

//example
int month_balance[12];

Month _balance is the array variable which will hold the 12 integers, which will represent the balance of each month.

Declaration of arrays in C++ can also be done in the following given manner,

int multiple[5] = {11,22,33,44,55};
char ex[10] = {'r', 'y', 't', 'i', 'e', 's', '\0'};

Accessing 1D array elements

Now, if we want to access the balance of month ‘April’, we simply had to mention the variable name followed by a square bracket containing the index value for the month of April.

‘month_balance[3]’

But as ‘April’ is the fourth month of the year, we mentioned ‘[3]’ (3 inside the square bracket) because all arrays have 0 as the index of their first element.

Declaration of 1-D Array in Java

In Java, this can be done as

//declaration in Java
type variable_name [];
variable_name = new type[size];

Here, initially, we had declared an array variable with its type, and then we had allocated memory to it using ‘new’ and assigned ‘new’ to the declared array variable. Let’s take the above given example if we want to declare an array which will contain the balance in each month of the year.

//example
int month_balance[];
month_balance= new int[12];

Here, ‘new’ allocates memory to array variable “month_balance”, so now, mont_balance will now hold the memory for 12 integer values.

Arrays can be initialized when they are declared. An array initializer is the list of values separated by commas and enclosed by curly braces.

//example
int month_balance={ 100, 500, 200, 750, 850,  250, 630, 248, 790, 360, 450,180 };

 Definition of Two-Dimensional Array (2-D array)

Both C++ and Java support multidimensional array. One of the simplest forms of a multidimensional array is a two-dimensional array or 2-D array. A two-Dimensional array can be expressed as ‘array of arrays’ or ‘array of one-dimensional arrays’.

To declare the two-dimensional array variable, we have to specify the array name followed by two square brackets where the second index is the second set of square brackets.

A two-dimensional array is stored in the form of the row-column matrix, where the first index designates the row and second index shows the column. The second or the rightmost index of an array alters very fastly as compared to the first or left-most index while accessing the elements of an array.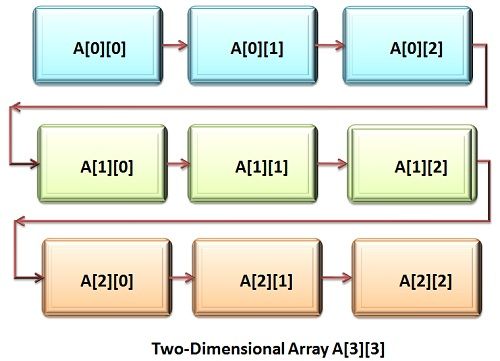

Declaration and Initialization of 2D Array in C++

In C++, the two-dimensional array is declared as;

//declaration in C++
type variable_name[size1][size2];

For example, we want to store the balance of every 30 days in each month of the year, in a 2-D array.

//example
int month_balance[12][30];

Initialization of 2D array is quite similar to the 1D array. The below-given example shows the 5×2 matrix of a 2D array.

int a[5][2] = { {0,2}, {1,4}, {2,6}, {3,8}, {4,10}};

Accessing 2D array elements

In order to access the entire 2D array in C++, we have to do looping against the rows and columns as shown below, then use “name_of_the_array[rows][coloumn]” for printing the elements of the array.

cout<<"The elements of the Array is: \n";
for(i=0; i<row; i++)
{
for(j=0; j<col; j++)
{
cout<<arr[i][j]<<" ";
}
cout<<"\n";
}

But, if you want to access just an element placed at some position then inside the square brackets in place of i and j, we can write the exact row and column number such as “arr[0][1]”.

Declaration of 2D Array in Java

In Java, the two-dimensional array is obtained by

//declaration in Java
type variable_name= new int[size1][size2];
//example
int month_balance= new int [12][30];

As we cannot pass the entire array as a parameter to a function, a pointer to the first element of the array is passed. An argument getting the two-dimensional array need to define its rightmost dimension. The rightmost dimension is required because the compiler needs it, to confirm the length of each row if it wants to index the array correctly. If the rightmost index is not mentioned, the compiler cannot determine where the next row starts.

//example in Java
void receiveing_funct( int a[][10]){
.
.
.
}

When the memory is dynamically being allocated to the two-dimensional array in Java, the left-most index is specified, and the remaining dimensions can be allocated separately, i.e. all rows of the array may not be of the same size.

//example in Java

int month_balance= new int[12][];

month_balance[0]= new int[31];
month_balance[1]= new int[28];
month_balance[2]= new int[31];
month_balance[3]= new int[30];
month_balance[4]= new int[31];
month_balance[5]= new int[30];
month_balance[6]= new int[31];
month_balance[7]= new int[30];
month_balance[8]= new int[31];
month_balance[9]= new int[30];
month_balance[10]= new int[31];
month_balance[11]= new int[30];
month_balance[12]= new int[31];

But there is no advantage of doing so.

Note

Passing of both, the one-dimensional array as well as, two-dimensional array to a function is similar, i.e. both are passed only by the name of the array.

//example
passing_funt(name_of_array);

Calculation of address

Implementation of One-Dimensional array

The address of any particular element in the 1D array can be calculated by the following equation,

Address of element a[k] = B+W*k

Here, B is the base address of the array, W is the size of each element of the array, and the number of elements needed in the array is k (i.e. index of element).

Example

For example, we wish to find the address of a 6th element of the one-dimensional array ‘a[10]’, whose base address is 1000. The size of each element in this example is 4 byte. So, the calculation based on this can be performed in the following way.

Address of element a[6] = 1000+4*6
= 1000+24
= 1024

Implementation of Two-Dimensional array

The address calculation in the 2D array is different from the 1D array due to the inception of the concept of rows and columns. There are two types of implementation-

• Row-major – In row-major the elements are read in row-wise fashion.
• Column-major – In column-major it is conducted column by column.

Row-major implementation

As we know, in this implementation, rows are stored one by one from first to the last. The formula used for computing the address of the elements in 2D array using row-major is:

Address of element a[i][j] = B + W (n(i-L1)+(j-L2))

Where B denotes the base address and W designates the size of each array element, and n is the number of columns. L1 specifies the lower bound of the row and L2 designates lower bound of the column.

Example

Suppose we need to find the address of the two-dimensional array residing at the location a[6,2] having base address 100 and defined as a[4…8, -2…3], which stores 2 bytes for each element.

Firstly we need to find the number of columns n, for which the upper bound of the defined array is subtracted from the lower bound, i.e., 3-(-2) and one is added to the result (as the indexing starts from 0), which gives 6.

Address of a[6][2] = 100+2(6(6-4)+(2-(-2)))
= 100+2(6×2+4)
= 100+32 = 132

Column-major implementation

The column-major implementation mainly differs from the row-major in the sense that it does the storage column by column. Its formula for calculating the address of an element is similar to the row-major except the column specifications has changed with row specifications.

Address of element a[i][j] = B + W (m(j-L2)+(i-L1))

Here, ‘m’ shows the number of rows.

Conclusion

In Both one-dimensional and two-dimensional array, the index plays a very important role because it is the only thing which specifically identifies an element in the array. Both one-dimensional and two-dimensional array can be initialized at the time of their declaration.