Difference Between B-tree and Binary tree (with Comparison Chart)

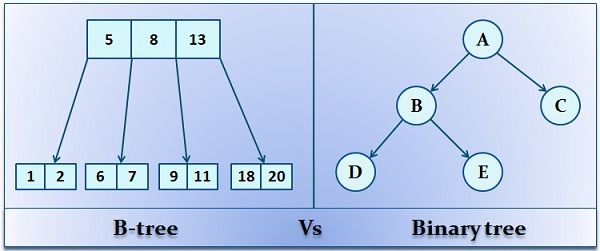
B-tree vs Binary tree B-tree and Binary tree are the types of non-linear data structure. Although the terms seem to be similar but are different in all aspects. A binary tree is used when the records or data is stored in the RAM instead of disk as the accessing speed of RAM is much higher than the disk. On the other hand, B-tree is used when the data is stored in the disk it reduces the access time by reducing the height of the tree and increasing the branches in the node.

Another difference between the B-tree and the binary tree is that B-tree must have all of its child nodes on the same level whereas binary tree does not have such constraint. A binary tree can have maximum 2 subtrees or nodes whereas in B-tree can have M no of subtrees or nodes where M is the order of the B-tree.

Comparison Chart

Basis for comparison	B-tree	Binary tree
Essential constraint	A node can have at max M number of child nodes(where M is the order of the tree).	A node can have at max 2 number of subtrees.
Used	It is used when data is stored on disk.	It is used when records and data are stored in RAM.
Height of the tree	log`_M` N (where m is the order of the M-way tree)	log`₂` N
Application	Code indexing data structure in many DBMS.	Code optimization, Huffman coding, etc.

Definition of B-tree

A B-tree is the balanced M-way tree and also known as the balanced sort tree. It is similar to binary search tree where the nodes are organized on the basis of inorder traversal. The space complexity of B-tree is O(n). Insertion and deletion time complexity is O(log n).

There are certain conditions that must be true for a B-tree:

The height of the tree must lie as minimum as possible.
Above the leaves of the tree, there should not be any empty subtrees.
The leaves of the tree must come at the same level.
All nodes should have least number of children except leave nodes.

Properties of B-tree of order M

Each node can have maximum M number of children and minimum M/2 number of children or any number from 2 to the maximum.
Each node has one key less than children with maximum M-1 keys.
The arrangement of the keys is in some specific order within the nodes. All keys in the subtree present in the left of the key are predecessors of the key, and that present in the right of the key are called successors.
At the time of insertion of a full node, the tree splits into two parts, and the key with median value is inserted at parent node.
Merging operation takes place when the nodes are deleted.

Definition of Binary tree

A Binary tree is a tree structure which can have at most two pointers for its child nodes. It means that the highest degree a node can have is 2 and there could be zero or one-degree node too.

There are certain variants of a binary tree such as strictly binary tree, complete binary tree, extended binary tree, etc.

The strictly binary tree is a tree where each non-terminal node must have left subtree and right subtree.
A tree is called a Complete Binary tree when it satisfies the condition of having 2 ⁱ nodes at each level where i is the level.
Threaded binary is a binary tree which consists of either 0 no of nodes or 2 number of nodes.

Traversal Techniques

Tree traversal is one of the most frequent operation performed on tree data structure in which each node visited exactly once in a systematic way.

Inorder: In this tree traversal the left subtree is visited recursively then root node is visited and in last right subtree is visited.
Preorder: In this tree traversal the root node is visited at first then left subtree and at last right subtree.
Postorder: This technique visits left subtree then right subtree and at last root node.

Key Differences Between B-tree and Binary tree

In B-tree, the maximum number of child nodes a non-terminal node can have is M where M is the order of the B-tree. On the other hand, a Binary tree can have at most two subtrees or child nodes.
B-tree is used when data is stored in disk whereas binary tree is used when data is stored in fast memory like RAM.
Another area of application for B-tree is code indexing data structure in DBMS, in contrast, Binary tree is employed in code optimization, huffman coding, etc.
The maximum height of a B-tree is log_MN (M is the order of tree). As against, binary tree maximum height is log₂N (N is the number of nodes and base is 2 because it is for binary).

Conclusion

The B-tree is used over binary and binary search tree the main reason behind this is the memory hierarchy where CPU is connected to cache with the high bandwidth channels while CPU is connected to disk through low bandwidth channel.

A binary tree is used when records are stored in RAM (small and fast) and B-tree are used when records are stored in disk (large and slow). So, use of B-tree instead of Binary tree significantly reduces access time because of high branching factor and reduced height of the tree.