 Normalization is a method that removes redundancy from a relation thereby minimizing the insertion, deletion and update anomalies that degrade the performance of databases. In this article, we will differentiate among two higher normal forms i.e. 3NF and BCNF.
Normalization is a method that removes redundancy from a relation thereby minimizing the insertion, deletion and update anomalies that degrade the performance of databases. In this article, we will differentiate among two higher normal forms i.e. 3NF and BCNF.
The basic difference between 3NF and BCNF is that 3NF eliminates the transitive dependency from a relation and a table to be in BCNF, the trivial functional dependency X->Y in a relation must hold, only if X is the super key.
Let us discuss the differences between 3NF and BCNF with the help of comparison chart shown below.
Content: 3NF Vs BCNF
Comparison Chart
| Basis for Comparison | 3NF | BCNF |
|---|---|---|
| Concept | No non-prime attribute must be transitively dependent on the Candidate key. | For any trivial dependency in a relation R say X->Y, X should be a super key of relation R. |
| Dependency | 3NF can be obtained without sacrificing all dependencies. | Dependencies may not be preserved in BCNF. |
| Decomposition | Lossless decomposition can be achieved in 3NF. | Lossless decomposition is hard to achieve in BCNF. |
Definition of 3NF
A table or a relation is considered to be in Third Normal Form only if the table is already in 2NF and there is no non-prime attribute transitively dependent on the candidate key of a relation.
So, before I address the process of normalizing a table in 3NF, allow me to discuss the candidate key. A Candidate Key is minimal super key i.e. a super key with minimum attributes that can define all attributes of a relation.
So, in the process of normalizing your table, first, you recognise the candidate key of a given relation. The attributes that are part of candidate key are prime attributes, and the attributes that are not the part of candidate key are non-prime attributes.
Now if we a relation R(A, B, C, D, E, F) and we have following function dependencies for the relation R.
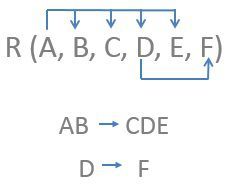 Observing functional dependencies, we can conclude that AB is a candidate key for relation R because using key AB we can search the value for all the attribute in a relation R. So A, B becomes prime attributes as they together make candidate key. The attributes C, D, E, F becomes non-prime attributes because none of them is the part of a candidate key.
Observing functional dependencies, we can conclude that AB is a candidate key for relation R because using key AB we can search the value for all the attribute in a relation R. So A, B becomes prime attributes as they together make candidate key. The attributes C, D, E, F becomes non-prime attributes because none of them is the part of a candidate key.
The table is in 2NF as no non-prime attribute is partially dependent on candidate key
But, a transitive dependency is observed among the functional dependencies provided, as the attribute F is not directly dependent on candidate key AB. Instead, attribute F is transitively dependent on candidate key AB via attribute D. Till attribute D has some value we can reach to attribute value of F, from the candidate key AB.
In case the value of attribute D is NULL we can never find/search the value of F with the help of candidate key AB. This is the reason why 3NF demands to remove the transitive dependency from the relations.
So, to remove this transitive dependency, we need to divide the relation R. While dividing a relation always place the candidate key, and all the attributes that depend on that candidate key in the first relation. In next divided relation, we will place the attribute that causes transitive dependency and also the attributes that depend on it in the second relation.
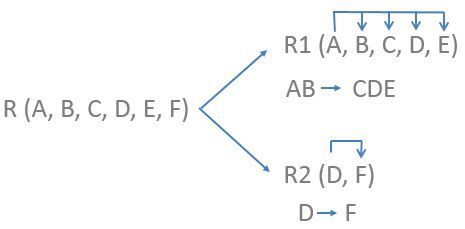 Now, the tables R1 and R2 are in 3NF as it has no partial and transitive dependencies left. Relation R1 (A, B, C, D, E) has a candidate key AB whereas, relation R2 (D, E) has D as its candidate key.
Now, the tables R1 and R2 are in 3NF as it has no partial and transitive dependencies left. Relation R1 (A, B, C, D, E) has a candidate key AB whereas, relation R2 (D, E) has D as its candidate key.
Definition of BCNF
BCNF is considered to be the stronger than 3NF. The relation R to be in BCNF must be in 3NF. And wherever a non-trivial functional dependency A -> B holds in relation R, then A must be a superkey of relation R. As we know, Super key is a key which has a single attribute or set of attributes that determines, the entire attributes of a relation.
Now, let us move on to an example to understand BCNF in a better way. Let us, suppose we have a relation R(A, B, C, D, F), which have following functional dependencies.
 By observing the relation R, we can say that A and BF are candidate keys of relation R, because they alone can search the value for all attributes in the relation R. So A, B, F are the prime attributes whereas, C and D are non-prime attributes. No transitive dependency is observed in the functional dependencies present above. Hence, the table R is in 3NF.
By observing the relation R, we can say that A and BF are candidate keys of relation R, because they alone can search the value for all attributes in the relation R. So A, B, F are the prime attributes whereas, C and D are non-prime attributes. No transitive dependency is observed in the functional dependencies present above. Hence, the table R is in 3NF.
But one functional dependency i.e. D -> F is violating the definition of BCNF, according to which, if D -> F exist then D should be the super key which is not the case here. So we will divide the relation R.
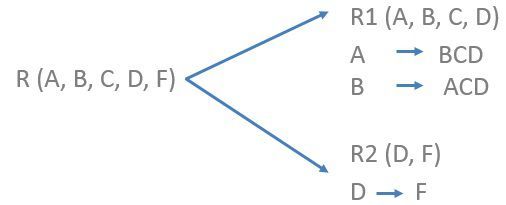 Now, the tables R1 nd R2 are in BCNF. Relation R1 has two candidate keys A and B, the trivial functional dependency of R1 i.e. A-> BCD and B -> ACD, hold for BCNF as A and B are the super keys for relation. Relation R2 has D as its candidate key and the functional dependency D -> F also holds for BCNF as D is a Super Key.
Now, the tables R1 nd R2 are in BCNF. Relation R1 has two candidate keys A and B, the trivial functional dependency of R1 i.e. A-> BCD and B -> ACD, hold for BCNF as A and B are the super keys for relation. Relation R2 has D as its candidate key and the functional dependency D -> F also holds for BCNF as D is a Super Key.
Key Differences Between 3NF and BCNF
- 3NF states that no non-prime attribute must be transitively dependent on the candidate key of the relation. On the other hands, BCNF states that if a trivial functional dependency X -> Y exist for a relation; then X must be a super key.
- 3NF can be obtained without sacrificing the dependency of relation. However, dependency may not be preserved while obtaining BCNF.
- 3NF can be achieved without loosing any information from the old table whereas, while obtaining BCNF we may loose some information from the old table.
Conclusion
BCNF is much restrictive than 3NF which help in normalizing the table more. The relation in 3NF has minimum redundancy left which is further removed by the BCNF.
nicomp says
Your 3NF example is not in 2NF. Not all non-prime attributes are dependent on the candidate key.
Vyshnavi says
Nice explanation thank you so much…
Stanisława Pałętka says
Good content….
Wang says
In BCNF decomposition, why we removed the second functional dependency?
Thanks
Sara says
Perfect.one of the best definitins for normalization rules.