Difference Between DDA and Bresenham line drawing algorithm

While drawing a line on computers they need to perform a set of computation, and it is not that simple as humans can do it in a simple way. So, in computer graphics, there are two algorithms used for drawing a line over the screen that is DDA (Digital Differential Analyser) algorithm and Bresenham algorithm. The chief difference between them is that the DDA algorithm uses floating point values while Bresenham employs integer with round off functions.

Furthermore, the implementation of the DDA algorithm involves multiplication and division while in bresenham algorithm, addition and subtraction are the main operations performed over the integers.

Content: DDA Algorithm Vs Bresenham Algorithm

1. 1. Comparison Chart
   2. Definition
   3. Key Differences
   4. Conclusion

Comparison Chart

Basis for comparison	DDA Algorithm	Bresenham Algorithm
Efficiency	Low	High
Calculations involved	Complex	Simple
Speed	Comparatively less	More
Operations used	Multiplication and division	Additions and subtraction
Arithmetic computation values	Floating point	Integer type
Precision	Low	High
Cost	Expensive	Moderate or cheaper relatively.
Optimization	Not provided	Provided

Definition of DDA Algorithm

A DDA (Digital Differential Analyzer) algorithms is a scan-conversion method for drawing a line which follows an incremental approach. In this algorithm to draw a line the difference in the pixel points is analysed then according to that the line is drawn. The method is said to be incremental because it performs computations at each step and uses the outcome of the previous step.

Before understanding DDA algorithm, we must understand what is a line and how it is defined? When two points in a plane connected by a line segment and falls under the line equation is known as a line. The line equation mentioned above is y=mx+b where m is the slope (i.e., m = Δy/Δx) and y is the intercept of the line (the value of y at the points of the line).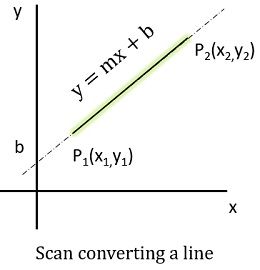

Now for DDA, let us assume at i we have computed (x_i, y_i) to be a point on the line as the next point (x_i+1, y_i+1) should Δy/Δx = m where Δy = (y_i+1) – y_i and Δx = (x_i+1) – x_i, which gives,

y_i+1 = y_i + mΔx or x_i+1 = x_i + Δy/m

Depending on the slope three types of situations can arise shown in the below-given diagram: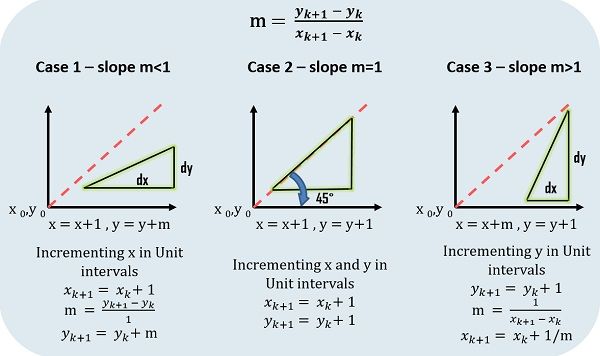It does not use the floating point multiplication. However, it uses the floating point addition which makes it faster than the straight implementation of the line equation. The algorithm is not precise because of the usage of floating point representation could cause computed points to drift away from their actual position when the line is relatively long.

Definition of Bresenham Algorithm

Bresenham algorithm also provides an efficient raster scan method for generating lines where incremental integer calculations are used. The developer of the algorithm was Jack Elton Bresenham, and the algorithm was named after him. It generates mathematically precise results with the help of addition, subtraction and multiplication by 2, which can be achieved by a simple arithmetic shift operation.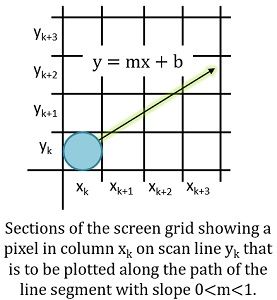

The above-given diagram explains the illustration of the straight line drawn over a display screen. Here the vertical axes indicate scan line positions, and the horizontal axes signify pixel columns. In the sampling at unit x intervals (as shown in example), we need to figure out which possible pixel positions lie nearer to the line path at each consequent step. So, this algorithm does it by examining the sign of an integer parameter, where its value is equal to the difference between the separation of the two pixel position from the true line path.

Now let’s understand Bresenham’s approach, considering a scan-conversion technique for lines having a positive slope of less than 1. Then the pixel location over the line path are then calculated by sampling at unit x intervals. It begins from the left endpoint (x₀, y₀) of a provided line, then each consecutive column (x position) is considered, and pixels are plotted where the scan-line y value is nearest to the line path. Suppose we have deduced that the pixel to be displayed at (x_k, y_k), then the next decision to ponder about is which pixel to plot in column x_k+1. We can select for the pixels at the given positions (x_k+1, y_k) and (x_k+1, y_k+1).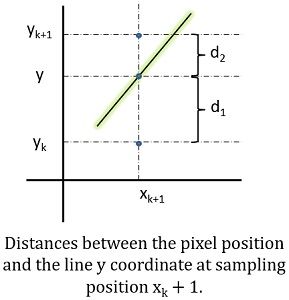

For the position xk+1, the vertical line path labelled as d₁ and d₂ from the mathematical line path. The y coordinate for pixel column position x_k+1 is deduced as
y = m (x_k+1) + b         –Eq 1
Then
d₁ = y-y_k = m (x_k+1) + b – y_k
and
d₂ = (y_k+1) – y = y_k+1 + m(x_k+1) – b

The difference between these two separations is

d1-d2 = 2m (x_k+1) – 2y_k +2b -1        –Eq 2

The decision parameter P_k for the kth iteration in the line algorithm is obtained by reordering 2nd equation and substituting Δy/Δx in place of m. Δy and Δx are the vertical and horizontal separation of the endpoints position.

P_k = Δ x (d₁ – d₂) = 2 Δy . x_k – 2 Δx . y_k + c        –Eq 3

Here the sign of P_k is equal to the d₁-d₂ as Δx is greater than 0. The value of the parameter c (constant) is 2Δy + Δx(2b-1) which does not affect the pixel position and can be removed in the recursive calculation of P_k. In some other cases, the pixel at y_k position could present near to the line path than a pixel at y_k+1 (i.e., d₁>d₂) and the parameter P_k is negative. In that condition, we plot the lower pixel. Otherwise, the upper pixel is plotted.

Integrated changes along the line occur in unit steps in any of the direction x or y. Therefore, the consequent decision parameters are calculated using an incremental approach. At k+1 iteration, the decision parameter is calculated from equation 3.

P_k+1 = 2Δy . x_k+1  –  2 Δx.y_k+1 + c

Subtracting equation 3 from the above equation, we get

P_k+1 – P_k = 2 Δy (x_k+1-x_k) – 2Δx(y_k+1 – y)
but x_k+1 = x_k+1, so that
P_k+1 = P_k + 2 Δy – 2 Δx (y_k+1 – y_k)

The term y_k+1 – y_k is either 0 or 1, according to the sign of parameter P_k. This iterative calculation of decision parameters is carried out at every integer x position, beginning from the left coordinate endpoint of the line. The first parameter P₀ is calculated from equation 3 at the pixel position (x₀,y₀) and m substituted as Δy/Δx.

P₀  =  2 Δy – Δx

Conclusion

The Bresenhem line drawing algorithm is more efficient and better in all aspects than the DDA algorithm which is not that efficient.