 Sorting is one of the major task in computer programs in which the elements of an array are arranged in some particular order. Sorting makes searching easier. Bubble sort and Selection sort are the sorting algorithms which can be differentiated through the methods they use for sorting. Bubble sort essentially exchanges the elements whereas selection sort performs the sorting by selecting the element.
Sorting is one of the major task in computer programs in which the elements of an array are arranged in some particular order. Sorting makes searching easier. Bubble sort and Selection sort are the sorting algorithms which can be differentiated through the methods they use for sorting. Bubble sort essentially exchanges the elements whereas selection sort performs the sorting by selecting the element.
Another considerable difference between the two is that bubble sort is stable algorithm while selection sort is an unstable algorithm. An algorithm is considered to be steady the elements with the same key occurring in the same order as they were occurring before sorting in the list or array. Generally, most stable and fast algorithms use additional memory.
Content: Bubble Sort Vs Selection Sort
Comparison Chart
| Basis for comparison | Bubble sort | Selection sort |
|---|---|---|
| Basic | Adjacent element is compared and swapped | Largest element is selected and swapped with the last element (in case of ascending order). |
| Best case time complexity | O(n) | O(n2) |
| Efficiency | Inefficient | Improved efficiency as compared to bubble sort |
| Stable | Yes | No |
| Method | Exchanging | Selection |
| Speed | Slow | Fast as compared to bubble sort |
Definition of Bubble Sort
Bubble sort is the simplest iterative algorithm operates by comparing each item or element with the item next to it and swapping them if needed. In simple words, it compares the first and second element of the list and swaps it unless they are out of specific order. Similarly, Second and third element are compared and swapped, and this comparing and swapping go on to the end of the list.
The number of comparisons in the first iteration are n-1 where n is the number elements in an array. The largest element would be at nth position after the first iteration. And after each iteration, the number of comparisons decreases and at last iteration only one comparison takes place.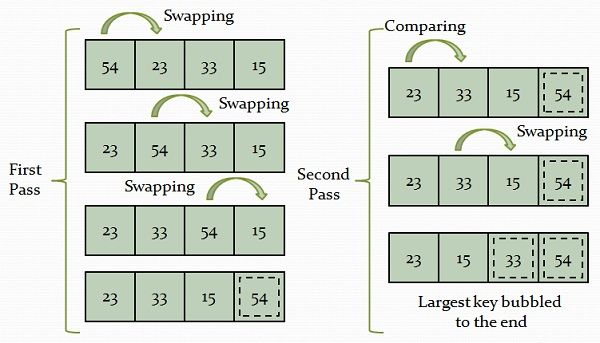
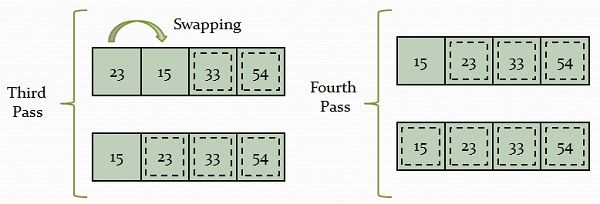
This algorithm is the slowest sorting algorithm. The best case complexity (When the list is in order) of the Bubble sort is of order n (O(n)), and worst case complexity is O(n2). In the best case, it is of order n because it just compares the elements and doesn’t swap them. This technique also requires additional space to store the temporary variable.
Definition of Selection Sort
Selection sort has achieved slightly better performance and is efficient than bubble sort algorithm. Suppose we want to arrange an array in ascending order then it functions by finding the largest element and exchanging it with the last element, and repeat the following process on the sub-arrays till the whole list is sorted.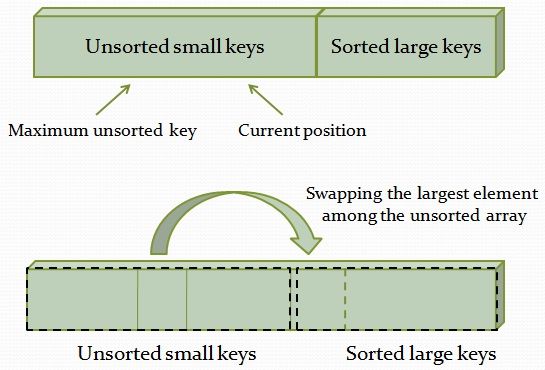 In selection sort, the sorted and unsorted array doesn’t make any difference and consumes an order of n2 (O(n2)) in both best and worst case complexity. Selection sort is faster than Bubble sort.
In selection sort, the sorted and unsorted array doesn’t make any difference and consumes an order of n2 (O(n2)) in both best and worst case complexity. Selection sort is faster than Bubble sort.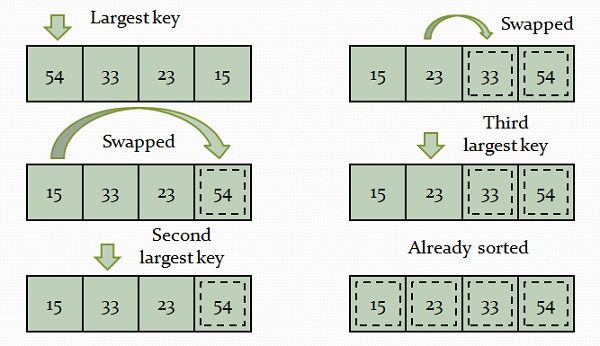
Key Differences Between Bubble Sort and Selection Sort
- In the bubble sort, each element and its adjacent element is compared and swapped if required. On the other hand, selection sort works by selecting the element and swapping that particular element with the last element. The selected element could be largest or smallest depending on the order i.e., ascending or descending.
- The worst case complexity is same in both the algorithms, i.e., O(n2), but best complexity is different. Bubble sort takes an order of n time whereas selection sort consumes an order of n2 time.
- Bubble sort is a stable algorithm, in contrast, selection sort is unstable.
- Selection sort algorithm is fast and efficient as compared to bubble sort which is very slow and inefficient.
Conclusion
Bubble sort algorithm is considered to be the most simple and inefficient algorithm, but selection sort algorithm is efficient as compared to bubble sort. Bubble sort also consumes additional space for storing temporary variable and needs more swaps.
Maya says
Nice presentation thank you.
baldguy says
Very nice
Peter says
Great article.
Sandesh Shrestha says
In selection sorting too, the method is interchanging. Can you explain this?
naveen says
nice and very useful…
KK says
Average and Worst case time complexity is О(n2) for Bubble sort!